导数——拐点偏移在高考中的应用
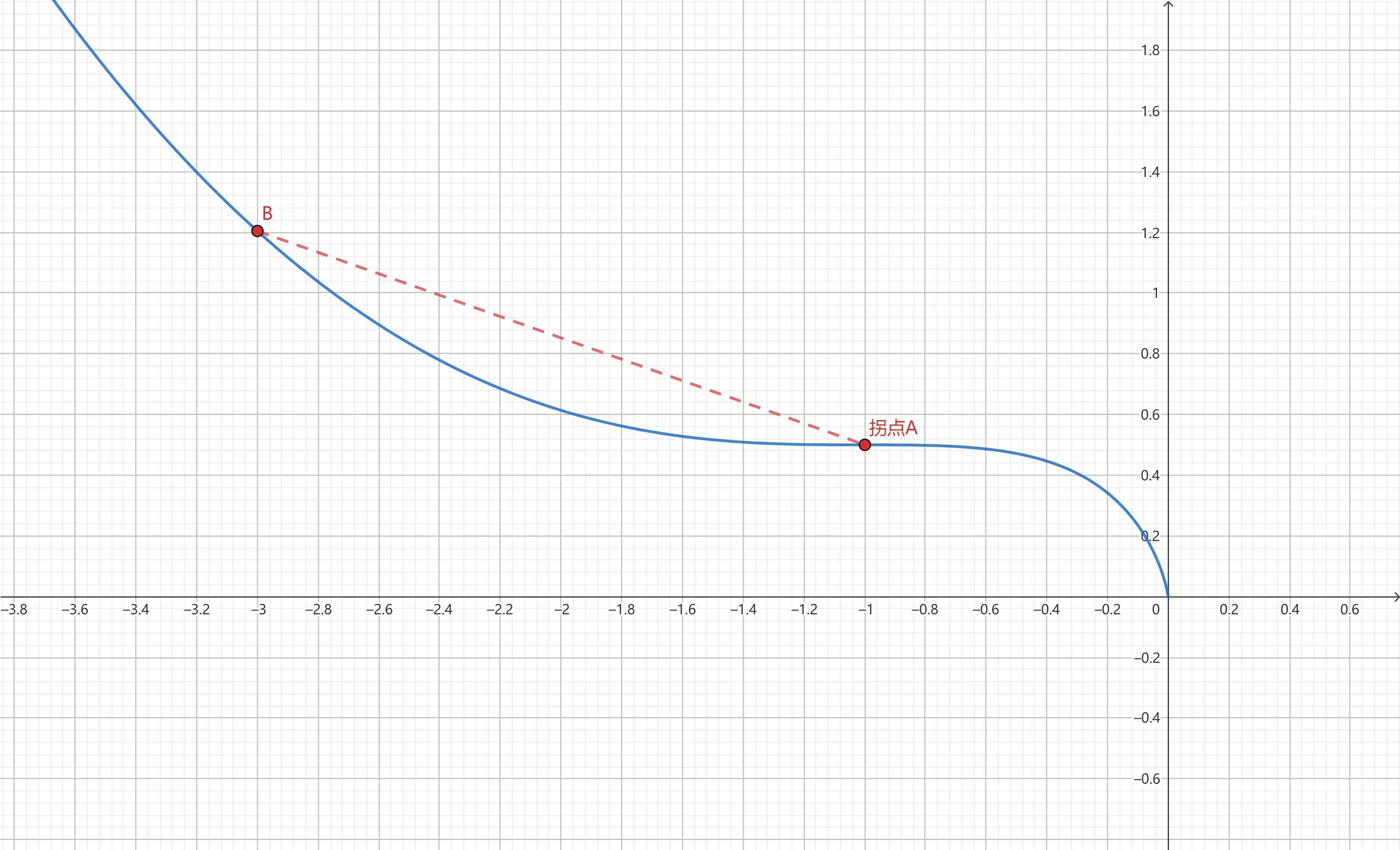
导数——拐点偏移在高考中的应用
Katorly知识点
$a,b\in D,f(\frac{a+b}{2})<\frac{f(a)+f(b)}{2}$
$k$先减后增,$f^{‘}(x)$先减后增
$k$先增后减,$f^{‘}(x)$先增后减
$\Rightarrow\color{Magenta}f^{‘’}(x)=0$
拐点:凹凸性改变的点(是个点)
$\color{Magenta}\begin{aligned}
&原f(x) &拐点\\
&导f^{‘}(x) &极值点\\
&二导f^{‘’}(x) &零点
\end{aligned}$
题型特点:$f(x)$相加为定值.
例题
例1
$\color{Cyan}已知f(x)=2\ln x+x^2+x. 若正实数x_1,x_2满足f(x_1)+f(x_2)=4,求证:x_1+x_2\geq2.$
$f^{‘}(x)=\frac{2}{x}+2x+1=\frac{2x^2+x+2}{x}>0\qquad f(x)递增$
$f^{‘’}(x)=-\frac{2}{x^2}+2=\frac{2x^2-2}{x^2}\qquad令f^{‘’}(x)=0\Rightarrow x=1$
$\therefore拐点:f(x)=2\qquad不妨设0<x_1<1<x_2$
$f(x_1)+f(x_2)=4\Rightarrow f(x_2)=4-f(x_1)$
$\therefore只需证x_1+x_2\geq2\Rightarrow x_2\geq2-x_1$
$\Leftrightarrow f(x_2)-f(2-x_1)\geq0\Leftrightarrow f(x_1)+f(2-x_1)\leq4$
$F(x)=f(x_1)+f(2-x_1)=$
$找出F(x)_{max}并证明其小于等于4即可.$
例2
$\color{Cyan}已知f(x)=x\ln x-\frac{1}{2}x^2,若f(x_1)+f(x_2)=-1,(x_1\neq x_2),证明:x_1+x_2>2.$
$f^{‘}(x)=\ln x+1-x\quad(x>0)$
$f^{‘’}(x)=\frac{1}{x}-1\qquad令f^{‘’}(x)=0\Rightarrow x=1$$\color{Magenta}\textit{(导为0求拐点)}$
$\therefore拐点f(1)={\color{Magenta}-\frac{1}{2}}\qquad不妨设x_1>1>x_2>0$
$只需证x_1+x_2>2\Rightarrow x_1{\color{Magenta}>}2-x_2$
$\Leftrightarrow f(x_1)-f(2-x_2){\color{Magenta}<}0$$\color{Magenta}\textit{(注意函数增减)}$$\color{Magenta}\textit{(将小的移到有常数的一边)}$
$\because f(x_1)+f(x_2)={\color{Magenta}-1}\Rightarrow f(x_1)=-1-f(x_2)$$\color{Magenta}\textit{(相加得到的$-1$为拐点$-\frac{1}{2}$的2倍)}$
$\therefore-1-f(x_2)-f(2-x_2)<0$
$\Leftrightarrow f(x_2)+f(2-x_2)>-1$
$\color{Magenta}\textit{(e.g. 证$2-f(x_2)-f(-x_2)<0$是不行的. 一定要把常数和函数分开,不然出不了结果)}$
$\Leftrightarrow x_2\ln x_2-\frac{1}{2}x_2^2+(2-x_2)\ln {(2-x_2)}-\frac{1}{2}(2-x_2)^2>-1$
$\Leftrightarrow F(x)=x\ln x-x^2+2x-2+(2-x)\ln {(2-x)}>-1$
$\begin{aligned}
F^{‘}(x)
&=\ln x+1-2x+1-\ln {(2-x)}\quad(0<x<1)\\
&=\ln x-\ln {(2-x)}-2x+1
\end{aligned}$
$\begin{aligned}
F^{‘’}(x)
&=\frac{1}{x}+\frac{1}{2-x}-2\\
&=\frac{2-x+x-2(2x-x^2)}{x(2-x)}\\
&=\frac{2(x-1)^2}{x(2-x)}>0
\end{aligned}$
$\therefore F^{‘}(x)递增\qquad F^{‘}(x)_{max}<F^{‘}(1)=-1$
$F(x)_{min}>F(1)=-1+2-2=-1.$
例3
$\color{Cyan}已知f(x)=e^x-\frac{1}{2}x^2-ax,a\in R.$
$\color{Cyan}a\leq1时,若x_1\neq x_2,f(x_1)+f(x_2)=2,求证:x_1+x_2<0.$
$a\leq1时,f(x)递增$
$f^{‘}(x)=e^x-x-a$
$f^{‘’}(x)=e^x-1\qquad令f^{‘’}(x)=0\Rightarrow x=0$
$\therefore拐点f(0)=1\qquad设x_1>0>x_2$
$\therefore f(x_1)=2-f(x_2)$
$只需证x_1+x_2<0\Rightarrow x_1<-x_2$
$\Leftrightarrow f(x_1)-f(x_2)<0$
$\Leftrightarrow2-f(x_2)-f(-x_2)<0$
$\Leftrightarrow f(x_2)+f(-x_2)>2$
$\begin{aligned}
\Leftrightarrow F(x)
&=e^x-\frac{1}{2}x^2+ax+\frac{1}{e^x}-\frac{1}{2}x^2+ax\\
&=e^x+e^{-x}-x^2>2
\end{aligned}$
$\begin{aligned}
F^{‘}(x)
&=e^x-e^{-x}-2x\\
&=e^x-\frac{1}{e^x}-2x\\
&=\frac{e^x(e^x-2x)-1}{e^x}
\end{aligned}$
$F^{‘’}(x)=e^x+e^{-x}-2\geq0$$\color{Magenta}\textit{(用均值不等式判断)}$
$\therefore F^{‘}(x)<F^{‘}(0)=0$
$F(x)递减\qquad\therefore F(x)>F(0)=1+1=2.$
$\color{Magenta}以上套路解法成立的条件:f(x_1)+f(x_2)=2f(x_0)\quad(x_0为拐点的x)$
$\color{red}\textit{(不能作为“是否是拐点题型”的判断依据.)}$
左右换元构造函数
$\color{Cyan}已知f(x)=\frac{2}{3}x^3-\frac{3}{2}x^2+\ln x为定义域上的增函数,设g(x)=f(x)-\frac{2}{3}x^3-4\ln x+6x,$
$\color{Cyan}且g(x_1)+g(x_2)=0,求证:x_1+x_2\geq2+\sqrt6.$
$\color{Magenta}\xcancel{\begin{aligned}
&g(x)=-\frac{3}{2}x^2-3ln x+6x\\
&g^{‘}(x)=-3x-\frac{3}{x}+6\\
&g{‘’}(x)=-3+\frac{3}{x^2}\qquad令g^{‘’}(x)=0\Rightarrow\frac{3}{x^2}=3\Rightarrow x=1\\
&\therefore拐点g(1)=-\frac{3}{2}+6=\frac{9}{2}
\end{aligned}}$
$\color{Magenta}\textit{此题为拐点体型的变形,因为$g(x_1)+g(x_2)\neq2g(1)$,所以不能用套路}$
$\because g(x_1)+g(x_2)=0$
$\Rightarrow-\frac{3}{2}x_1^2-3\ln x_1+6x_1-\frac{3}{2}x_2^2-3\ln x_2+6x_2=0$
$\Rightarrow-\frac{3}{2}(x_1^2+x_2^2)+6(x_1+x_2)-3\ln{x_1x_2}=0$
$(x_1+x_2)[-\frac{1}{2}(x_1+x_2)+2]=\ln{x_1x_2}-x_1x_2$
$\color{Magenta}\textit{(把$x_1+x_2$、$x_1x_2$各放一边)}$
$令t=x_1x_2\quad\therefore右边=\ln t-t=h(t)\quad(t>0)$$\color{Magenta}\textit{(换元掉不要的)}$
$h^{‘}(t)=\frac{1}{t}-1\quad\therefore h(t)<-1$
$令b=x_1x_2\quad\therefore左边=-\frac{1}{2}b^2+2b\Rightarrow-b^2+4b\leq-2\Rightarrow b^2-4b-2\geq0$
$\color{Magenta}\textit{(再换掉要的(为方便观察))}$
$\Rightarrow b\geq2+\sqrt6(负值舍去)$
$\color{Magenta}拐点题型中若只有x、\ln x或x和\ln x都有但相互独立(即不是x\ln x、\frac{\ln x}{x}等)时都可用此法求解.$