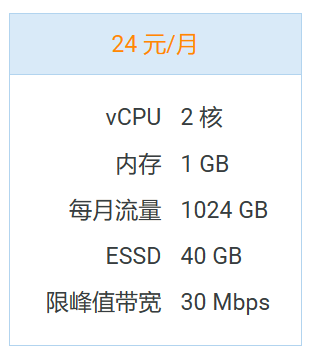
导数——隐零点在高考中的应用

Katorly2022-07-15

知识点

此处“零点”一般指$f^{‘}(x)=0$的零点.
不好求出确定数值时，利用零点存在定理卡出零点范围，最后想办法消掉或化简.

$\color{Cyan}已知f(x)=x+\ln x，g(x)=x+\ln x-xe^x-1. 证明：f(x)\leq g(x).$

$只需h(x)=f(x)-g(x)=x+\ln x-xe^x+1\leq0\quad(x>0)$

$h^{‘}(x)=1+\frac{1}{x}-e^x-xe^x=(x+1)(\frac{1}{x}-e^x)$$\color{Magenta}\textit{（$\frac{1}{x}-e^x$可用于求出零点方程）}$

$\because x>0\quad\therefore舍x=-1$

$\therefore令F(x)=\frac{1}{x}-e^x\quad(x>0)$

$\because F(\frac{1}{2})>0,F(1)<0$$\color{Magenta}\textit{（猜数代入与0比大小）}$

$\therefore存在x_0\in(\frac{1}{2},1)，使F(x)=0$

$\therefore\frac{1}{x_0}-e^x_0=0$

$x\in (0,x_0)时,h^{‘}(x)>0\Rightarrow h(x)递增$

$x\in (x_0,+\infty)时,h^{‘}(x)<0\Rightarrow h(x)递减$

$\therefore h(x)_{max}=h(x_0)=x_0+\ln x_0-x_0e^{x_0}+1$

$\because\frac{1}{x_0}-e^{x_0}=0\Rightarrow\begin{cases}
x_0e^{x_0}=1\\
取对\Rightarrow x_0=-\ln x_0\color{Magenta}\textit{（消除/化简）}
\end{cases}$

$\therefore h(x_0)=-1+1\leq0\quad得证.$

$\color{Cyan}已知f(x)=e^{x+a}-\ln x，证明：当a>1-\frac{1}{e}时，f(x)>e+1.$

$f^{‘}(x)=e^{x+a}-\frac{1}{x}$

$令f^{‘}(x)=0\Rightarrow\frac{1}{x}-e^{x+a}=0$

$\because f^{‘}(1)>0,f^{‘}(\frac{1}{e^{a+1}})<0$

$\therefore存在x_0\in(\frac{1}{e^{a+1}},1)，使f^{‘}(x)=0$

$\therefore f(x)_{min}=f(x_0)=e^{x_0+a}-\ln x_0$

$\frac{1}{x_0}-e^{x_0+a}=0\quad取对\Rightarrow-\ln x_0=x_0+a$

$易知f(x_0)递减\qquad\therefore f(x_0)>f(\frac{1}{e})=e+1.$

$\color{Cyan}已知f(x)=ax^2-ax-x\ln x，且f(x)\geq0.$
$\color{Cyan}当a=1时，证明：f(x)存在唯一的极大值点x_0，且e^{-2}<f(x_0)<2^{-2}.$

$f(x)=x^2-x-x\ln x\geq0\quad(x>0)$

$f^{‘}(x)=2x-1-\ln x-1=2x-\ln x-2$

$f^{‘}(x)=0\quad极小$

$f^{‘’}(x)=2-\frac{1}{x}$

$\therefore x_0\in(0,\frac{1}{2}$

$f^{‘}(x_0)=2x_0-\ln x_0-2=0$$\color{Magenta}\textit{（将$f(x_0)$作为一个函数）}$

$\begin{aligned}
\therefore f(x)_{max}
&=f(x_0)=x_0^2-x_0-x_0\ln x_0\\
&=-x_0^2+x_0\in(0,\frac{1}{4})
\end{aligned}$

$\therefore f(x_0)<2^{-2}$

$现只需-x_0^2+x_0>e^{-2}$

$\because f(\frac{1}{e})=\frac{1}{e^2}+\frac{1}{e}>\frac{1}{e^2}$

$又f^{‘}(\frac{1}{e})\neq0$

$\therefore f(x_0)>e^{-2}.$