导数——放缩法在高考中的应用

知识点

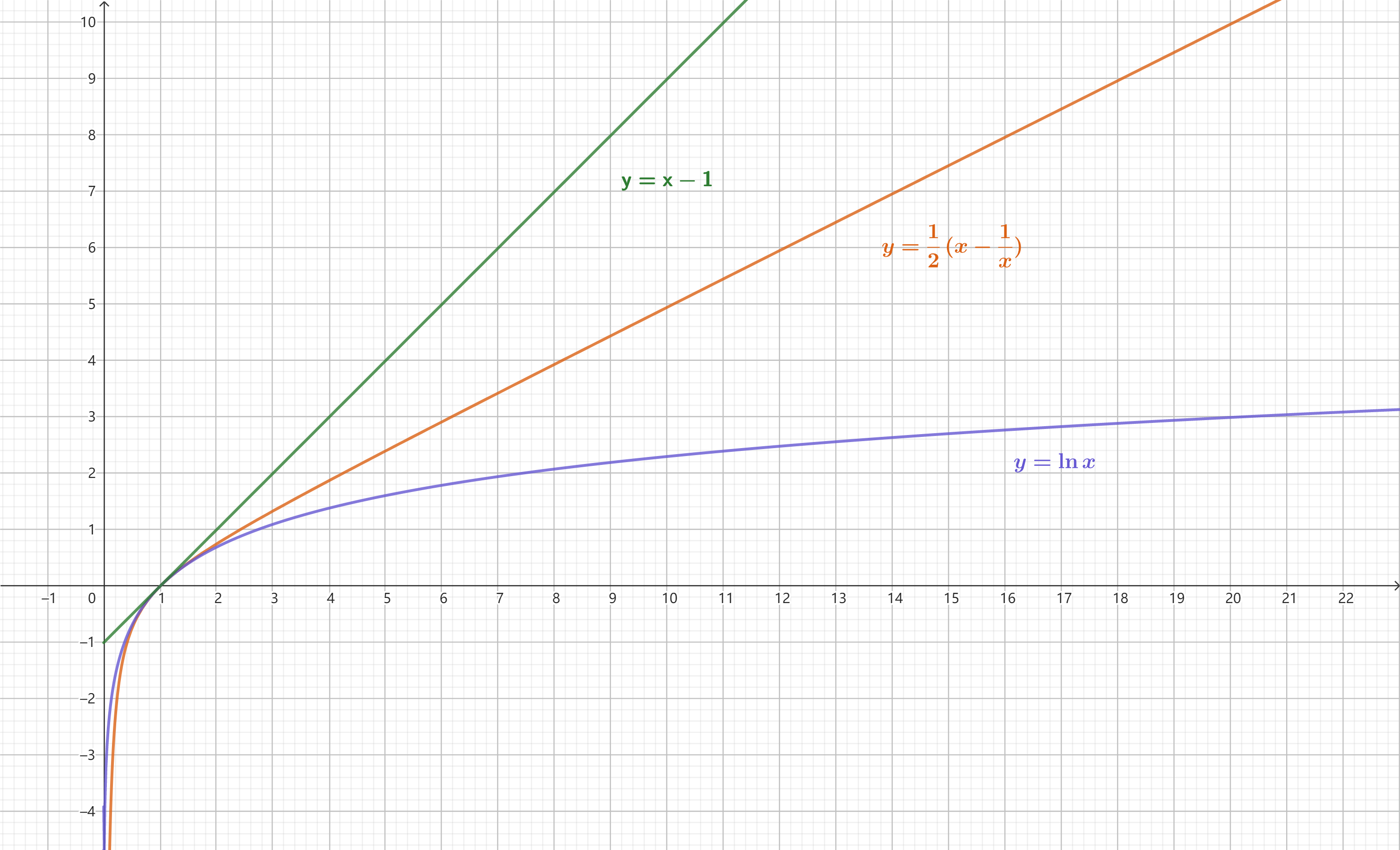
${\color{Magenta}e^x\geq x+1} \quad当x=0时取“=”$

${\color{Magenta}x-1\geq\ln x} \quad当x=1时取“=”$

$近年来\ln x<\frac{1}{2}(x-x\frac{1}{x})<x-1\textit{（新增）}$

$证明：e.g.\quad e^x-x-1\geq 0\quad证其最小值大于等于0即可.$

例题

例1

$\color{Cyan}若x,y是实数，e^{x+y+2}-3\leq \ln(y-2x+1)+3x，则2x+y=\underline{\phantom{answer}}.$

$\textit{x+y}\leq e^{x+y+2}-3\leq \ln (y-2x+1)+3x\leq \textit{x+y}$

$\therefore取“=”$

$\therefore\begin{cases}
x+y+2=0\\
y-2x+1=1
\end{cases}\Rightarrow\begin{cases}
x=-\frac{2}{3}\\
y=-\frac{4}{3}
\end{cases}$

$\therefore 2x+y=-\frac{8}{3}.$

例2

$\color{Cyan}实数x,y满足2x=\ln {(x+y-1)}+\ln {(x-y-1)}+4，则2020x^2+2019y^2=\underline{\phantom{answer}}.$

$\ln {(x+y-1)}\leq x+y-2$

$\ln {(x-y-y)}\leq x-y-2$

$\therefore 2x=\ln {(x+y-1)}+\ln {(x-y-1)}+4\leq 2x$

$\because取“=”$

$\therefore\begin{cases}
x+y-1=1\\
x-y-1=1
\end{cases}\Rightarrow\begin{cases}
x=2\\
y=0
\end{cases}$

$\therefore 2020x^2+2019y^2=8080.$

例3

$\color{Cyan}设m为整数，且对于任意正整数n，(1+\frac{1}{2})(1+\frac{1}{2^2})(1+\frac{1}{2^3})\dotsm(1+\frac{1}{2^n})<m，求m最小值.$
$\color{Magenta}\textit{（用$\ln x\leq x-1$来构造，因为有乘法）}$

$\begin{aligned}
\ln x\leq x-1
&\Rightarrow \ln {(x+1)}\leq x\\
&\Rightarrow \ln {(x+\frac{1}{2^k})}\leq\frac{1}{2^k}
\end{aligned}$

$\therefore\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\dotsm+\frac{1}{2^n} = 1-(\frac{1}{2})^n<1$

$\begin{aligned}
&\therefore取对\ln (\frac{1}{2}+1)+\ln (\frac{1}{2^2}+1)+\dotsm+\ln (\frac{1}{2^n}+1)\\
&=\ln (1+\frac{1}{2})(1+\frac{1}{2^2})(1+\frac{1}{2^n})\\
&<e<3
\end{aligned}$

$\therefore m>3.$

例4

$\color{Cyan}函数f(x)=e^x-\ln {(x+m)}，求证：当m\leq 2时，f(x)>0.$

$\color{Magenta}\xcancel{\begin{aligned}
&e^x-\ln {(x+m)}>0\qquad \ln {(x+m)}\leq x+m-1\\
&e^x-\ln {(x+m)}>x+1-\ln {(x+m)}\\
&>x+1-x-m+1>2-m\geq 0
\end{aligned}}$

$\color{Magenta}\textit{$e^x$和$\ln {(x+m)}$两者取等条件不一样$\quad\therefore$不可同时用}$

$e^x\geq x+1\geq\ln {(x+2)}\geq\ln {(x+m)}$

$\because等号不同时成立$

$\therefore e^x>\ln{(x+m)}\Rightarrow e^x-\ln{(x+m)}>0.$