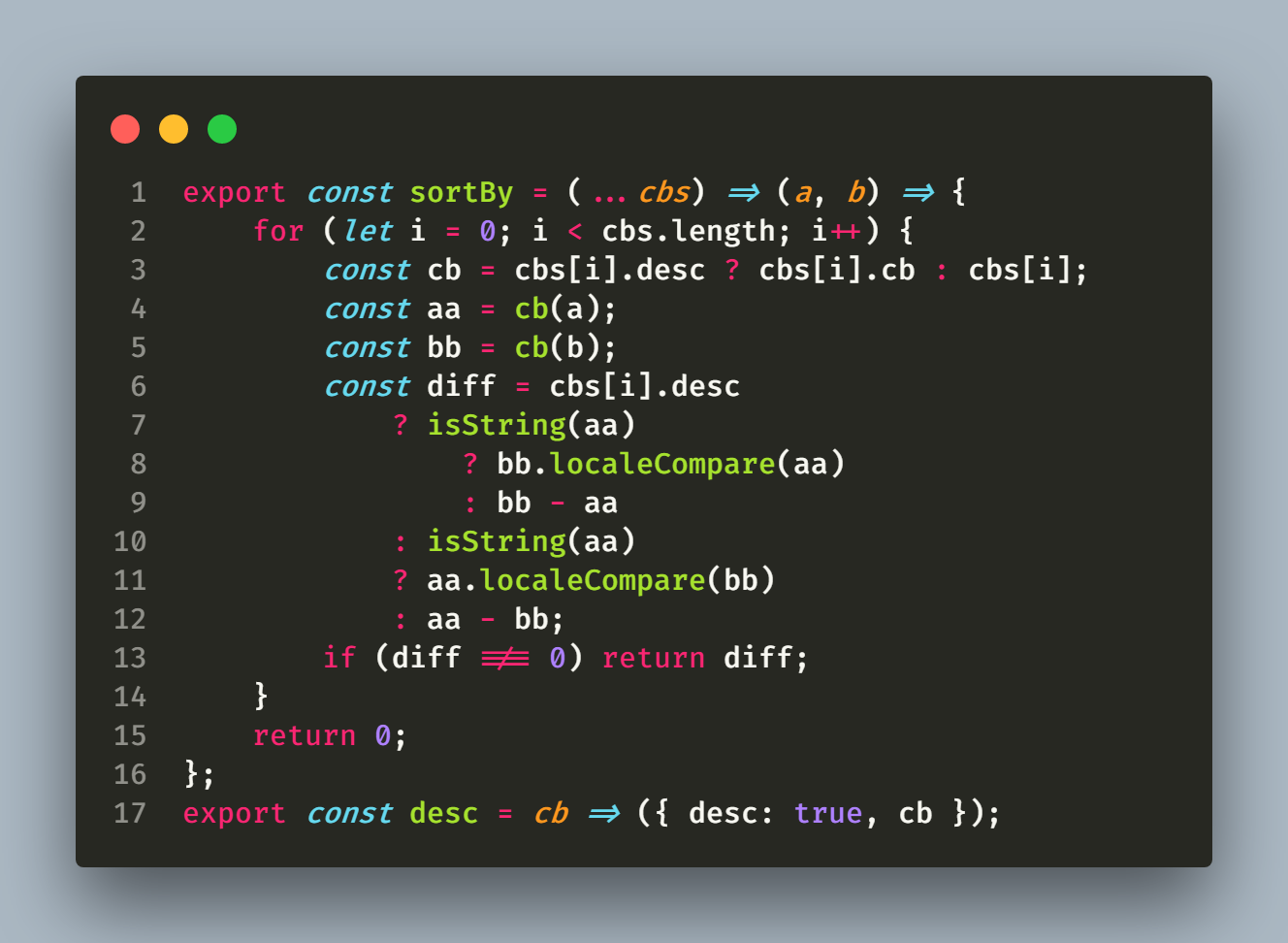
导数——极值点方程消参在高考中的应用

Katorly2022-07-14

知识点

双极值点问题 $\Rightarrow f^{‘}(x)=0两根为x_1,x_2 \Rightarrow 用韦达\begin{cases}
对称式 &\color{Magenta}消x_1,x_2,留a\\
非对称式 &\color{Magenta}消a,留x_1/x_2
\end{cases}$
$\textit{（非对称式：看系数，把$x_1,x_2$互换后看是否与原来一致}$
$\textit{$\qquad e.g.\ x_1+x_2、f(x_1)+f(x_2)、\frac{f(x_1)+f(x_2)}{x_1-x_2}$为对称式}$
$\textit{$\qquad\qquad x_1-x_2、f(x_1)+2f(x_2)$为非对称式）}$

$\quad\color{Magenta}开口、端点、对称轴、\triangle \begin{cases}
x_1+x_2 = \\
x_1\cdot x_2 =
\end{cases}\quad含a$

$\textit{（构造的新函数必单调）}$

单极值点问题 $\Rightarrow f^{‘}(x)=0根为x_0 \Rightarrow 利用f^{‘}(x)=0方程 \color{Magenta}消a留x_0$

例题

例1

$\color{Cyan}设f(x)=\ln x+x^2-ax\ (a \in R)存在两个极值点x_1,x_2,且x_1<x_2,若0<x_1<\frac{1}{2}，$
$\color{Cyan}求证：f(x_1)-f(x_2)>\frac{3}{4}-\ln 2.$$\color{Magenta}\textit{（非对称式）}$

$f^{‘}(x)=\frac{1}{x}+2x-a=\frac{2x^2-ax+1}{x}$

$令f^{‘}(x)=0 \quad(x>0)$

$由韦达定理 \begin{cases}
x_1+x_2=\frac{a}{2} \\
x_1\cdot x_2=\frac{1}{2}
\end{cases} \Rightarrow a=2x_1+2x_2, \quad x_2=\frac{1}{2x_1}$

$\begin{aligned}
\therefore f(x_1)-f(x_2) &=\ln x_1+x_1^2-ax_1-\ln x_2-x_2^2+ax_2\\
&=\ln \frac{x_1}{x_2}+x_1^2-x_2^2-2(x_1^2-x_2^2)\\
&=\ln 2x_1^2-x_1^2+\frac{1}{4x_1^2}\\
&=\ln 2+\ln x^2-x^2+\frac{1}{4x^2}\\
&=g(x)\quad x\in(0,\frac{1}{2})
\end{aligned}$
$\color{Magenta}\textit{（留$x_1$，因为范围确定）}$

$g^{‘}(x)=\frac{-(2x^2-1)^2}{2x^3}<0$

$\therefore g(x)在(0,+\infty)递减$

$\therefore g(x)_{min}>g(\frac{1}{2})=-\ln 2-\frac{1}{4}+1=\frac{3}{4}-\ln 2.$

例2

$\color{Cyan}已知f(x)=e^x+\ln x-x, g(x)=ae^x-\frac{1}{2}x^2-1.$
$\color{Cyan}当a>0时，若F(x)=af(x)-g(x)存在两极值点x_1,x_2，$ 0
$\color{Cyan}且x_1\neq x_2，求证：F(x_1)+F(x_2)<-2.$$\color{Magenta}\textit{（对称式）}$

$F(x)=\frac{1}{2}x^2+a(\ln x-x)+1 \quad(x>0)$

$F^{‘}(x)=x+\frac{a}{x}-a=\frac{x^2-ax+a}{x} \quad令F^{‘}(x)=0$

$由韦达定理 \begin{cases}
x_1+x_2=a \\
x_1\cdot x_2=a
\end{cases}$

$\begin{aligned}
\therefore F(x_1)+F(x_2)
&=\frac{1}{2}x_1^2+a(\ln x_1-x_1)+\frac{1}{2}x_2^2+a(\ln x_2-x_2)+2\\
&=-\frac{1}{2}a^2+a\ln a-a+2\\
&=h(a)
\end{aligned}$

$h^{‘}(a)=\ln a-a<0$

$\therefore h(a)递减$

$又\because \triangle=a^2-4a>0 \Rightarrow a\in (4,+\infty)$$\color{Magenta}\textit{（满足$F(x)$存在两极值点 $\Rightarrow$ 使$F^{‘}(x)=0$有两解）}$

$\therefore h(a)_{max}=h(4)=4(\ln 4-1)<-2.$

例3

$\color{Cyan}若f(x)=x^2-x+a\ln x\quad (a>0)存在两个极值点，$
$\color{Cyan}证明\frac{f(x_1)-f(x_2)}{x_1-x_2}>4a-\frac{1}{2}.$

$f^{‘}(x)=2x-1+\frac{a}{x}=\frac{2x^2-x+a}{x}$

$\therefore \frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{x_1^2-x_1+a\ln x_1-x_2^2+x_2-a\ln x_2}{x_1-x_2}$

$令f^{‘}(x)=0\quad 由韦达定理\begin{cases}
x_1+x_2=\frac{1}{2}\\
x_1\cdot x_2=\frac{1}{2}a
\end{cases} \Rightarrow a=2x_1x_2,\quad 2x_1+2x_2=1$

$\begin{aligned}
\therefore \frac{f(x_1)-f(x_2)}{x_1-x_2}
&=\frac{(x_1+x_2-1)(x_1-x_2)+a\ln \frac{x_1}{x_2}}{x_1-x_2}\\
&=-\frac{1}{2}+\frac{x_1x_2(\ln x_1-\ln x_2)}{x_1-x_2}
\end{aligned}$

$只需证-\frac{1}{2}+\frac{x_1x_2(\ln x_1-\ln x_2)}{x_1-x_2}>4a-\frac{1}{2}=8x_1x_2-\frac{1}{2}$

$\Leftrightarrow \frac{\ln x_1-\ln x_2}{x_1-x_2}>4=8(x_1+x_2)$

$不妨设x_1<x_2$$\color{Magenta}\textit{（这样好确定$\frac{x_1}{x_2}$的范围）}$

$\Leftrightarrow \ln \frac{x_1}{x_2}<\frac{2(\frac{x_1}{x_2}-1)}{\frac{x_1}{x_2}+1}$

$令t=\frac{x_1}{x_2}，则t\in (0,1)$

$\Leftrightarrow h(x)=\ln t-\frac{2(t-1)}{t+1}<0$

$h^{‘}(x)=\frac{1}{t}-\frac{2}{(t+1)^2}=\frac{t^2+1}{t(t+1)^2}>0$

$\therefore h(x)递增\quad \therefore h(x)_{max}<h(1)=0.$
$\color{Magenta}\textit{“只需证”之后其实为套路，对数平均不等式：}$
$\color{Magenta}\qquad \frac{x_1+x_2}{2}>\frac{x_1-x_2}{\ln x_1-\ln x_2}$