导数——极值点偏移在高考中的应用
导数——极值点偏移在高考中的应用
Katorly知识点
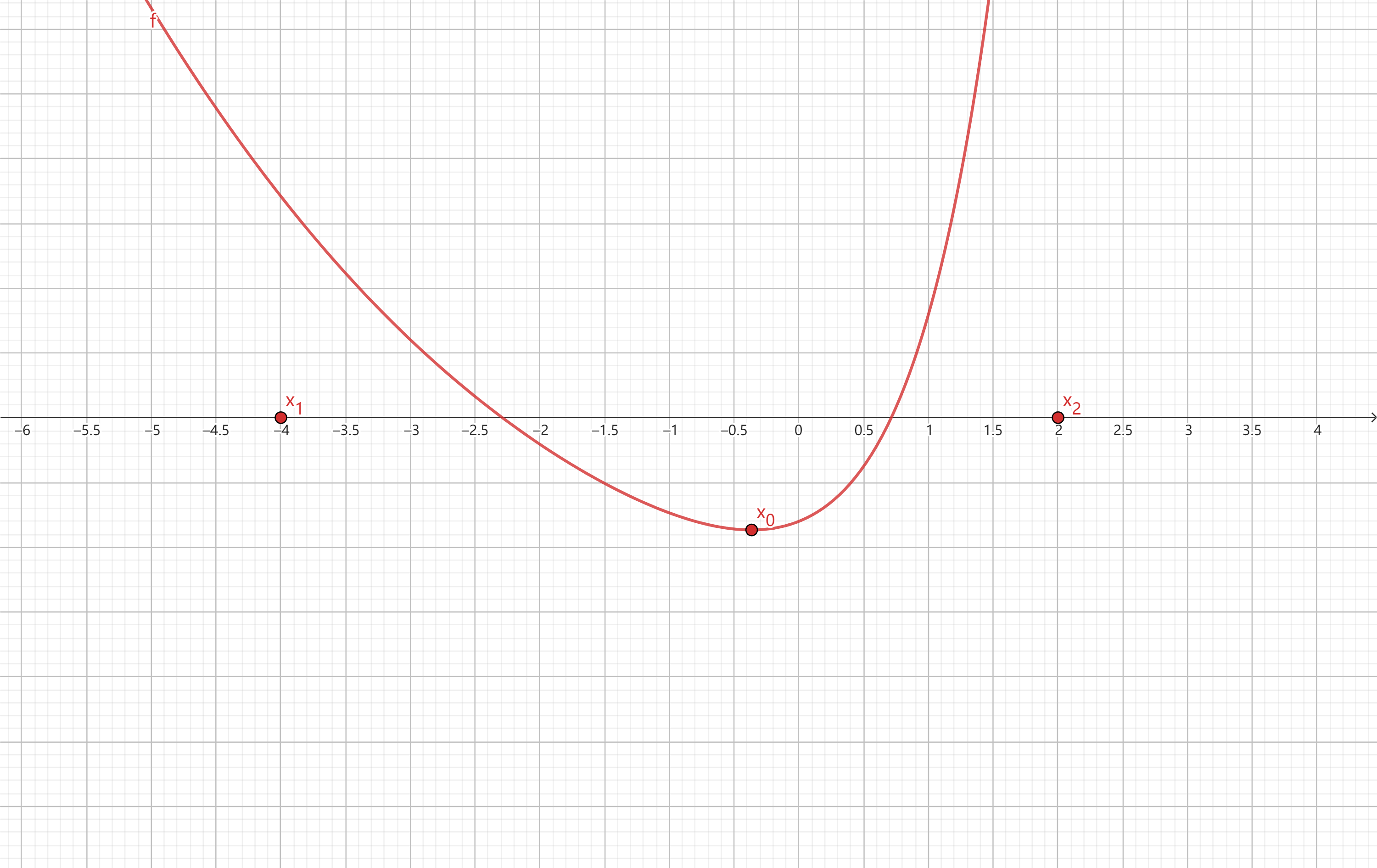
$f(x)=m$ 有2零点 $x_1, x_2, (f(x_1)=f(x_2)), f(x)$ 极值点为 $x_0$,求证 $x_1+x_2 >或< 2x_0$
极值点偏右:$x_1+x_2<2x_0$
(联想中点公式)
极值点偏左:$x_1+x_2>2x_0$
步骤(套路)(以左图为例):
$\color{Magenta}\textbf{判单调}$ $f(x)$ 在 $(-\infty,x_0)$ 递减,$(x_0, +\infty)$ 递增
$\color{Magenta}\textbf{转移区间}$ 不妨设 $x_1<x_0<x_2$,只需证 $x_2<2x_0-x_1$ (将小的那一项移向极值点那一边)
$\color{Magenta}\textbf{套 f(x)}$
$\because f(x)在(x_0,+\infty)递增$$\therefore只需证f(x_2)<f(2x_0-x_1)$
$又\because f(x_1)=f(x_2)$
$\therefore f({\color{Magenta}x_1})<f(2x_0-{\color{Magenta}x_1})$
$\color{Magenta}\textit{(使只有一个变量)}$$\color{Magenta}\textbf{构造函数(必单调)}$
$g(x)=f(x_1)-f(2x_0-x_1),x=x_1\in(-\infty,x_0)$$只需证g(x)<0在(-\infty,x_0)恒成立即可$
$g(x)_{min}<0.$
例题
例1
${\color{Cyan}已知 (0,+\infty) 上 f(x)=\frac{1}{2}x^3-mx+1 存在两个零点 x_1, x_2. 其中 m>\frac{3}{2},求证:x_1+x_2>2.}$
$f^{‘}(x)=\frac{3}{2}x^2-m \quad令f^{‘}(x)=0 \Rightarrow x_0=\frac{\sqrt{6m}}{3}>1(舍负)$
$不妨设x_2>x_0>x_1 \therefore只需证x_2>2-x_1$
$\Leftrightarrow f(x_2)>f(2-x_1) \Leftrightarrow \frac{1}{2}x_1^3-mx_1-\frac{1}{2}(2-x_1)^3-m(2-x_1)>0$
$\Leftrightarrow x^3-3x^2+6x-4-2m=F(x)$
$F^{‘}(x)=3x^2-6x+6>0 \therefore F(x)递增$
$\therefore f(x_2)>f(2-x_1) \Rightarrow x_1+x_2>2$
例2
$\color{Cyan}已知 f(x)=(x-2)e^x+a(x-1)^2 有两个零点.$
$\color{Cyan}(1) 求 a 的取值范围.$
$\color{Cyan}(2) 设 x_1,x_2 是其两个零点,证明:x_1+x_2<2.$
$(1) 令 f(x)=0 \Rightarrow -a=\frac{(x-2)e^x}{(x-1)^2}=g(x)$
$g^{‘}(x)=\frac{e^x(5-2x)}{(x-1)^3}$$\color{Magenta}\textit{(参变分离,当两个函数求有交点的范围时用)}$
$x \rightarrow -\infty \Rightarrow g(x) \rightarrow 0$
$x \rightarrow 1 \Rightarrow g(x) \rightarrow -\infty$
$x \rightarrow +\infty \Rightarrow g(x) \rightarrow +\infty$
$\therefore -a<0 \Rightarrow a>0$.
$(2) f^{‘}(x)=e^x(x-1)+2a(x-1)=(e^x+2a)(x-1)$
$令f^{‘}(x)=0 \Rightarrow x_0=1$
$不妨设x_2>1>x_1$
$只需证x_1+x_2<2 \Leftrightarrow x_2<2-x_1$
$\Leftrightarrow f(x_1)<f(2-x_1)$
$\Leftrightarrow (x-2)e^x+xe^{2-x}=F(x)$
$F^{‘}(x)=(e^x-\frac{e^2}{e^x})(x-1)$
$\because x=x_1<1$
$\therefore F^{‘}(x)<0$
$\therefore F(x) 递增$
$\therefore f(x_1)<f(2-x_1) \Rightarrow x_1+x_2<2$.
例3
$\color{Cyan}已知 f(x)=x\ln x 的图像与直线 y=m 交于不同的两点 A(x_1,y_1),B(x_2,y_2),求证:x_1 \cdot x_2<\frac{1}{e^2}.$
$\color{Magenta}\textit{(极值点偏移的变形)}$
$不妨设0<x_2<\frac{1}{e}<x_1$
$f^{‘}(x)=\ln x+1,令f^{‘}(x)=0$
$\Rightarrow x=\frac{1}{e} \quad\therefore极小值为\frac{1}{e}$
$\therefore x_1\cdot x_2<\frac{1}{e^2} \Rightarrow x_1<\frac{1}{x_2e^2}$$\color{Magenta}\textit{(移小的)}$
$\begin{aligned}
只需证F(x)
&=f(x_1)-f(\frac{1}{x_2e^2})<0
&{\color{Magenta}\textit{(余下的与极值点偏移相同)}}\\
&=x_1\ln x_1+\frac{1}{x_1e^2}\ln x_1e^2<0\\
&=x\ln x+\frac{1}{xe^2}\ln xe^2<0
\end{aligned}$
$\begin{aligned}
F^{‘}(x)
&=\ln x+1-\frac{1}{x^2e^2}\ln xe^2\\
&=(\ln x+1)(1-\frac{1}{x^2e^2})>0 \quad(0<x<\frac{1}{e})
\end{aligned}$
$\therefore F(x)递增$
$\therefore F(x)_{max}<F(\frac{1}{e})=0 \quad得证$.